Практическая электротехника
Практическая электротехника  Однофазные цепи переменного синусоидального тока
Однофазные цепи переменного синусоидального тока  Цепь переменного тока с активной и индуктивной нагрузкой
Цепь переменного тока с активной и индуктивной нагрузкой
Цепь переменного тока с активной и индуктивной нагрузкой
| Практическая электротехника - Однофазные цепи переменного синусоидального тока |
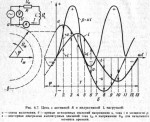
Реальная катушка индуктивности обычно имеет и активное сопротивление, которым нельзя пренебречь. На рисунке 6.7, а показана цепь катушки, индуктивность которой L, а активное сопротивление R. На рисунке 6.7, б изображены кривые мгновенных значений напряжения и и тока i в цепи R и L, а на рисунке 6.7, в — взаимное расположение векторов напряжения Um и тока 1т, сдвинутых относительно один другого на угол φ.
Если в цепи с R и L проходит синусоидальный ток i = Im sin ωt, то мгновенное значение активной составляющей напряжения может быть определено как uа = Ri = RIm sin ωt. Мгновенное значение напряжения на индуктивном сопротивлении в соответствии с формулой (6.18).
uL = XL Im sin (ωt + Π/2). (6.23)
Мгновенное же значение напряжения, приложенного ко всей цепи, равно алгебраической сумме мгновенных значений напряжений на активном и индуктивном сопротивлениях:
u = uа + uL = RIm sinωt + XLImsin(ωt + Π/2). (6.24)
Так как оба слагаемых этой суммы — синусоидальные величины, изменяющиеся с одинаковой частотой га, то результирующее напряжение и тоже синусоидально и имеет ту же частоту.
Это результирующее напряжение u представлено на рисунке 6.7, б. Векторная диаграмма амплитудных значений напряжения и тока приведена на рисунке 6.7, в.
Анализ схем с несколькими сопротивлениями в цепи удобно проводить на векторных диаграммах действующих значений величин, которые могут быть измерены приборами, например вольтметром и амперметром (рис. 6.7, а). Для перехода к диаграмме амплитудных величин каждый вектор действующего значения следует увеличить в √2 раз, так как Um = √2u, а Im = √2I.
Порядок построения векторной диаграммы для схемы 6.7, а таков. Общим для обоих сопротивлений R и XL в этой схеме является ток, действующее значение которого измеряют амперметром А. Откладываем этот ток в определенном, удобном для нас, масштабе (рис. 6.8, а) по горизонтали, так как начальная фаза тока i = Im sin ωt равна нулю (рис. 6.7, б). Напряжение Ua, совпадает по фазе с током, поскольку оно приложено к участку цепи, имеющему только активное сопротивление R. Поэтому вектор Ua откладываем вдоль вектора İ. Масштаб напряжения также выбираем удобным для построения. Например, если для тока мы приняли масштаб 1:1, то есть 1 ампер отложили в 1 см длины вектора İ, то для напряжения удобнее принять масштаб 100:1, то есть 100 вольт отложить в 1 см.
Напряжение UL опережает ток I по фазе на угол Π/2, так как оно приложено к участку цепи, имеющему только индуктивное сопротивление. Поэтому вектор ÚL отложим в направлении, перпендикулярном вектору İ. Причем масштаб вектора UL должен быть равен масштабу Ua. Складывая затем геометрически Úa, и ÚL, получим вектор действующего значения общего напряжения U, приложенного к цепи с R и XL.
На векторной диаграмме (рис. 6.8, а) векторы Úa, ÚL и Ú образуют прямоугольный треугольник, который называют треугольником напряжений.
По теореме Пифагора для этого треугольника
U = √Ua2 + UL2 (6.25), где √ - корень квадратный;
Если все стороны треугольника напряжений разделить на величину I, то получится так называемый треугольник сопротивлений (рис. 6.8, б). Из этого треугольника
Z = √R2 + XL2 = √R2 + (ωL)2, (6.26)где Z — полное сопротивление всей цепи, Ом.
Если известно напряжение U, приложенное к исследуемой цепи (оно может быть измерено вольтметром V на рисунке 6.7, а), а также ток в цепи I (он измеряется амперметром А), то полное сопротивление всей цепи
Z = U/I,
отсюда
Формула (6.2) является математическим выражением закона Ома для цепи с индуктивной и активной нагрузкой, с последовательным соединением индуктивного и резистивного элементов. Пользуясь векторными диаграммами, можно написать следующие соотношения между составляющими напряжения и найти значение угла φ. Так, из рисунка 6.8, а
Пример 1. Определить полное сопротивление, ток и угол сдвига фаз между напряжением сети и током в цепи, если активное сопротивление цепи R = 50 Ом, индуктивность катушки, включенной последовательно с активным сопротивлением, L = 0,5 Г, частота тока ƒ = 50 Гц, напряжение V = 220 В. Решение. Индуктивное сопротивление
XL = ωL = 2ΠƒL = 2•3.14•50•0,5 = 157 Ом.
Полное сопротивление
Z = √R2 + XL2 = √2500 + 24 649 = 165 Ом.
Ток в цепи
График мгновенных значений мощности, которую потребляет цепь с активным и индуктивным сопротивлениями, можно получить способом, изложенным при рассмотрении цепи с активным сопротивлением. С этой целью для ряда моментов времени (1, 2, ... 13) определяют мгновенные значения тока, i и напряжения и (рис. 6.7, б), а затем, перемножив их, находят мгновенные значения мощности р. Расчет сводят в таблицу.
Мгновенное значение мощности в цепи с активным и индуктивным сопротивлениями можно также определить аналитически:
Второй член полученного выражения описывается периодической кривой, изменяющейся с двойной частотой по сравнению с частотой тока и напряжения. Как было показано выше (см. § 6.3), при таком характере кривой ее среднее значение за период равно нулю.
Поэтому, переходя к средним значениям, получим среднюю мощность цепи, которую называют ее активной мощностью:
Р = UI cosφ. (6.31)
Характер мощностей и соотношение между ними в схеме с активным и индуктивным сопротивлениями можно установить, если все стороны треугольника напряжений умножить на действующее значение тока I. При этом образуется треугольник мощностей (рис. 6.8, в). Из этого треугольника активная мощность, измеряемая, как известно, в ваттах или киловаттах,
Ра = UaI = UI cosφ = S cosφ, (6.32)
то есть результат тот же, что и при аналитическом определении. Реактивная мощность, измеряемая, как указывалось выше, в вольтамперах реактивных (вар) или киловольт-амперах реактивных (квар),
QL = UL I = Ul sinφ = S sinφ. (6.33)
Полная мощность
S = UI = √U2I2 = √(IUa)2 + (IUL)2 = √P2 + QL2. (6.34)
Полную мощность измеряют в вольт-амперах (В•А) или киловольт-амперах (кВ• А).
Косинус фи (cosφ) в цепи с индуктивностью в практике часто называют отстающим или положительным.
На активном сопротивлении выделяется активная мощность Р = UаI = I2R, а индуктивное сопротивление определяет значение реактивной мощности, как
QL = ULI = I2ωL. (6.35)
В практике активную мощность измеряют ваттметром, а полную мощность подсчитывают как произведение показаний. вольтметра и амперметра. Зная эти две величины, можно рассчитать реактивную мощность. Величину coscp называют также коэффициентом мощности. Практически в электроустановках cosφ определяют, пользуясьпоказаниями ваттметра (или счетчика с пересчетом киловатт-часов в киловатты), вольтметра и амперметра, или измеряют специальным прибором фазометром. Отношение показаний ваттметра произведению показаний вольтметра на показания амперметра дает значение коэффициента мощности:
| < Предыдущая | Следующая > |
|---|
| Похожие материалы: |
|---|
Кстати, тоже интересно почитать:
- Цепь переменного тока с индуктивной нагрузкой
- Цепь переменного тока с емкостной нагрузкой
- Цепь переменного тока с параллельно соединенными приемниками энергии
- Включение нагрузки в трехфазную сеть
- Графики нагрузок источника электроснабжения
- Годовые графики и их анализ
- Номинальные первичное и вторичное напряжения
- Группы соединения обмоток трансформатора
- Параллельная работа трансформаторов
- Выбор сечения проводов по условиям нагрева
- Расчет проводов на потерю напряжения