Практическая электротехника
Практическая электротехника  Однофазные цепи переменного синусоидального тока
Однофазные цепи переменного синусоидального тока  Цепь переменного тока с индуктивной нагрузкой
Цепь переменного тока с индуктивной нагрузкой
Цепь переменного тока с индуктивной нагрузкой
| Практическая электротехника - Однофазные цепи переменного синусоидального тока |
Если в цепь переменного тока включена идеальная индуктивность, то в момент времени, когда возрастает мгновенное значение силы тока, протекающего от источника, энергия источника расходуется на образование магнитного поля в индуктивности без превращения ее в тепловую или механическую энергию. В момент времени, когда мгновенное значение силы тока убывает, магнитное поле рассеивается, и запасенная в нем энергия отдается обратно источнику.
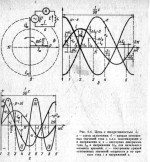
Покажем это аналитически и графически. Пусть к источнику переменного тока подключена катушка индуктивностью L (рис. 6.6, а).
Примем, что ее активное сопротивление R равно нулю. В катушке будет протекать переменный синусоидальный ток
i = Im sin ωt.
Этот ток сопровождается переменным синусоидальным магнитным потоком, совпадающим с ним по фазе. Переменный магнитный поток, образующийся в катушке, индуктирует э. д. с. самоиндукции eL, пропорциональную скорости изменения тока (потока), аналогично формуле (5.10):
где eL - э.д.с. самоиндукции, B; ∆i/∆t - скорость изменения тока, А/с; L - индуктивность катушки в, Г.
Знак минус отражает правило Ленца, которое в данном случае означает, что если мгновенное значение тока увеличивается (то есть его приращение за время ∆t имеет положительный знак: + ∆i — точки 1 и 5 на рисунке 6.6, б), то мгновенное значение э.д.с. будет иметь отрицательный знак: — L (+∆i/∆t) =—eL. Если же мгновенное значение тока уменьшается (то есть его приращение за время At имеет отрицательный знак: —Ai — точки 3 и 4 на рисунке 6.6,6), то э. д. с. имеет положительный знак: — L (—∆i/ ∆t) = + eL .
Таким образом, исходя из этих соображений, можно построить кривую мгновенных значений э. д. с. самоиндукции на основании имеющейся развернутой диаграммы тока.
Как показано на рисунке 6.6, б, в момент времени, соответствующий точке 1, приращение тока положительное: +i2—( + i1)=+∆i1. В момент времени 5 это приращение также положительное: +∆i5. Следовательно, мгновенные значения э.д.с. в эти моменты отрицательные: —e1 и —е5. В момент времени 2 приращение тока равно нулю: ∆i2 = i4 —i3 = 0, поэтому и э.д.с. е2 равна нулю, то есть в этот момент график э.д.с. проходит через нуль и меняет свой знак с минуса на плюс. В моменты времени, соответствующие точкам 3 и 4, приращение токов Ai3 и Ai4 отрицательно (например, для точки 3: i6 — i5 =—∆i3). В эти моменты времени знаки э.д.с. положительны (+е3 и +е4).
Применяя второй закон Кирхгофа для цепи, изображенной на рисунке 6.6, а, и принимая во внимание, что в этой цепи действует напряжение источника и и э.д.с. самоиндукции eL, можно написать:
u + eL = 0 или eL = —u. (6.15)
Значит, развернутая диаграмма напряжения будет зеркальным отображением развернутой диаграммы э.д.с, так как только в этом случае в каждый момент времени сумма значений э.д.с. и напряжений равна нулю.
Теперь по развернутой диаграмме напряжения и тока можно построить векторную диаграмму их максимальных значений, например для начального момента времени (рис. 6.6, в). Из векторной диаграммы • видно, что в цепи с индуктивностью ток отстает от напряжения на угол φ = 90° = Π/2 рад. В соответствии с графиком, то есть если ток определяется равенством i = I sinωt, напряжение u = Um sin(ωt + Π/2). Это можно показать и аналитически. А именно, из формул (6.14) и (6.15).
u = — е= L∆i/∆t. (6.16)
Чтобы перейти к действующим значениям U и I, в этой формуле необходимо раскрыть значение ∆i/∆t. Это представляется возможным сделать с привлечением аппарата тригонометрии. Если в момент времени t мгновенное значение силы тока i = I sin ωt, то для момента времени t + ∆t (∆t — весьма малый, близкий к нулю, отрезок времени) ток изменится на весьма малую величину ∆i и будет равен:
i + ∆i = Im sin ω(t + ∆t).
Преобразуя это равенство относительно ∆i, получим:
∆i = Im sin (ωt + ω∆t)— l = Im sin(ωt + ω∆t)—Im sin ωt = Im[sin(ωt + ω∆t)—sin ωt] = Im[sinωt-cosω∆t + cosωt•sinω∆t—sinωt]. (6.17)
В этом выражении угол ω∆t очень незначителен, так как ∆t по условию весьма малая величина. Тогда cosω∆t ≈ cos 0 = 1, a sin ω∆t ≈ ω∆t. Подставляя эти значения в формулу (6.17), получим:
∆i = Im(sinωt•1 + cosωt•ω∆t—sinωt) = Imω∆t cosωt,
откуда
∆i/ ∆t = Imωcosωt = Imsin(ωt + Π/2).
Напряжение на индуктивности
u = L∆i/∆t = Im Lsin(ωt + Π/2) = Um sin(ωt + Π/2). (6.18)
Из формулы (6.18) следует, что максимальное значение напряжения на индуктивности
Um = Imω L.
Поделив обе части этого равенства на √2 перейдем к действующим значениям тока и напряжения в цепи с индуктивностью:
или
где XL = U/I— индуктивное сопротивление.
Размерность индуктивного сопротивления — Ом:
[Х] = [ω][L] = 1/c• Г = 1/с Ом•с = Ом.
Индуктивное сопротивление в отличие от активного называют реактивным, то есть таким, в котором происходит обратимый процесс колебания энергии от источника электрической энергии к катушке индуктивности и обратно. Равенство (6.19) выражает закон Ома для цепи с индуктивной нагрузкой.
Мгновенная мощность в катушке в любой момент времени
Р = ui = Um sin(ωt + Π/2)Im sin ωt = Um Im cos ωt • sin ωt,
а учитывая, что
2 sin ωt • cos ωt = sin2ωt,
откуда
cosωt•sinωt = sin2ωt/2,
получим
P = UmIm /2 •sin2ωt = Um Im/√2√2 •sin 2ωt,
или
P = U I sin 2ωt . (6.20)
Таким образом, мгновенная мощность цепи с индуктивным сопротивлением изменяется с двойной частотой, в течение периода 2 раза достигая положительного максимума (рис. 6.6, г, моменты времени 2 и б) и 2 раза отрицательного максимума при том же абсолютном значении (моменты времени 4 и 8). В течение полупериодов I и III индуктивность потребляет от генератора мощность на образование магнитного поля. В течение полупериодов II н IV мощность имеет отрицательный знак. В эти полупериоды ток в цепи уменьшается до нуля и запасенная в магнитном поле индуктивной катушки энергия возвращается обратно в источник.
Положительным мгновенное значение мощности р в полуперирд I получается благодаря тому, что ток +i и напряжение +u в этот момент положительны (обе кривые лежат выше оси ωt). Для полупериода II ток положителен (+ i), а напряжение отрицательно (—u), поэтому мощность имеет отрицательный знак. Для полупериода III ток и напряжение имеют знак минус (—i, —u) и т. д.
Кривую мгновенных значений мощности можно было бы получить также графическим путем. При этом нужно найти мгновенные значения мощности для ряда точек (1, 2, У)— произведения мгновенных значений u и i, как это было проведено для цепи с активным сопротивлением.
Среднее значение мощности за период в соответствии с рисунком 6.6, г равно нулю, так как при сложении всех положительных и отрицательных значений мгновенной мощности р, изменяющейся по синусоиде, получается сумма, равная нулю. Другими словами, в цепи с индуктивностью происходит периодический обмен энергией между генератором и индуктивностью цепи без превращения электрической энергии в тепловую или механическую. Энергия магнитного поля в джоулях, запасаемая за четверть периода,
Wm = L Im2/2, (6.21)
где L — индуктивность катушки, Г; Im — максимальная сила тока, А.
Во время полупериодов II к IV катушка отдает запасенную магнитным полем энергию обратно источнику. Мера обмена энергией между источником и индуктивной катушкой — это максимальное значение мгновенной мощности, называемое реактивной мощностью:
QL = UI = I2XL = ω LI2, (6.22)
где U — действующее значение напряжения, определяемое по показанию вольтметра, В; I — действующее значение реактивного тока, А; ω — угловая частота, рад/с; L — индуктивность катушки, Г.
Реактивную мощность в отличие от активной измеряют в вольт-амперах, называемых реактивными вольт-метрами:
1 вольт-ампер реактивный (1 вар) = 1 вольт•1 ампер.
| < Предыдущая | Следующая > |
|---|
| Похожие материалы: |
|---|