Практическая электротехника
Практическая электротехника  Трехфазные цепи переменного тока
Трехфазные цепи переменного тока  Соединение источников тока
Соединение источников тока
Соединение источников тока
| Практическая электротехника - Трехфазные цепи переменного тока |
Если имеются два источника однофазного тока, каждый из которых дает 220 В, то их можно использовать или отдельно, как показано на рисунке 7.4,а, или соединив их, как показано на рисунке 7.4,6. В первом случае необходимы четыре провода, а во втором случае только три, но потребитель получает в свое распоряжение два напряжения: 220 В и 400 В.
Таким образом, система, показанная на рисунке 7.4, б, имеет два существенных преимущества: три провода вместо четырех и два напряжения вместо одного.
Аналогичное, экономически целесообразное соединение мы можем использовать в системе трех однофазных токов, сдвинутых друг относительно друга и меняющихся по одному и тому же закону. В каждое мгновение алгебраическая сумма трех э.д.с. равна нулю. Обратимся к диаграмме э.д.с, генерируемых в трех фазах (см. рис. 7.2). Для точки 1 (120°) э.д.с. еb в фазе В максимальна и положительна (направлена вверх от нулевой линии ординат). Э.д.с. в фазах А и С соответственно еа и ес имеют отрицательное значение, и каждая из них, как видно из рисунка, в 2 раза меньше по абсолютному значению, чем еb. Складывая все три э.д.с, получим нуль. Аналогично для точки 2 э.д.с. еа в фазе 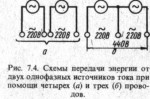 А имеет максимальное отрицательное значение, а э.д.с. еb и ес положительны, но их абсолютные значения в 2 раза меньше, чем абсолютное значение Складывая все три э.д.с, получаем в результате нуль. Для точки 3 Э.Д.С еа=0, а э.д.с. еb и ес равны по значению, но противоположны по знаку. В сумме они дают нуль.
А имеет максимальное отрицательное значение, а э.д.с. еb и ес положительны, но их абсолютные значения в 2 раза меньше, чем абсолютное значение Складывая все три э.д.с, получаем в результате нуль. Для точки 3 Э.Д.С еа=0, а э.д.с. еb и ес равны по значению, но противоположны по знаку. В сумме они дают нуль.
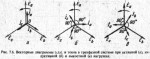
Тот же результат мы получим от геометрического сложения векторов трех э.д.с, если представим себе три однофазные э.д.с. в виде звезды одинаковых по длине векторов Ё, сдвинутых один относительно другого на угол 120° и вращающихся с частотой 50 об/с.
В каждый момент времени геометрическая сумма их будет равна нулю. К вектору Éb приложены вектор Éc и вектор Éa, сумма их равна нулю (получился замкнутый треугольник) (рис. 7.5, а). Это положение векторов соответствует моменту 1 на диаграмме (см. рис. 7.2). Спроектировав на вертикальную ось все три э.д.с, получим картину векторов, ранее взятую из диаграммы для точки 1. Повернув векторы на угол 60°, придем к диаграмме векторов на рисунке 7.5, б. Их проекции на вертикальную ось повторяют картину векторов, взятую из диаграммы рисунка 7.2 для точки 2. Повернув звезду векторов еще на угол 90°, придем к диаграмме на рисунке 7.5, в, соответствующей картине значений э.д.с. для точки 3 на диаграмме рисунка 7.2.
Аналогично будут изменяться и токи в трех фазах, если нагрузки на каждой из них равны между собой. И в каждый момент их алгебраическая сумма будет равна нулю. Если нагрузки в фазах активные, то звезда токов совпадает со звездой э.д.с. (рис. 7.6, а). Когда в каждую фазу включено чисто индуктивное сопротивление., ток в каждой фазе отстает от э.д.с. на 90° (рис. 7.6, б). Если нагрузка емкостная, токи в фазах опережают э.д.с. на 90° (рис. 7.6, в).
Поскольку алгебраическая сумма токов в трех фазах
ia + ib + ic = 0, (7.1)
то в каждый момент времени сумма токов в двух любых фазах равна по абсолютному значению, но противоположна по знаку току в третьей фазе.
Следовательно, из равенства (7.1) можно заключить:
ia = — ib—ic; ia + ib = —ic; (7.2)
ib + ic = —ia и т. д.
То есть ток, который в любой момент вытекает из какой-либо фазы, равен сумме токов, возвращающихся в две другие фазы, и наоборот. Так, для точки 1 (см. рис. 7.2) ток в фазе В идет во внешнюю цепь, а по фазам А и С возвращается к источнику и т. д. Рассмотренные выше зависимости между э.дх. (напряжениями) и токами для трехфазной системы позволяют соединять фазы в этих системах по специальным схемам, получившим названия «звезда» и «треугольник».
| < Предыдущая | Следующая > |
|---|
| Похожие материалы: |
|---|